Fast computation of the marginal likelihood for the Normal-Inverted Wishart model.

This is the numerator of the Bayes factor: assume that all observations come from the same source. Implemented in C.

marginalLikelihood(
  X,
  n.iter,
  B.inv,
  W.inv,
  U,
  nw,
  mu,
  burn.in,
  output.mcmc = FALSE,
  verbose = FALSE,
  Gibbs_only = FALSE
)

Arguments

X	the observation matrix ($n \times p$: n = observation, p = variables) @param U covariance matrix for the mean ($p \times p$)
n.iter	number of MCMC iterations excluding burn-in
B.inv	prior inverse of between-source covariance matrix
W.inv	initialization for prior inverse of within-source covariance matrix
nw	degrees of freedom
mu	prior mean ($p \times 1$)
burn.in	number of MCMC burn-in iterations
output.mcmc	if TRUE output the entire chain as a coda object, else just return the log-ml value
verbose	if TRUE, be verbose
Gibbs_only	if TRUE, only return the Gibbs posterior samples. Implies `chain_output = TRUE`.

Value

the log-marginal likelihood value, or a list:

value: the log-ml value
mcmc: a coda object with the posterior samples

Details

See diwishart_inverse for the parametrization of the Inverted Wishart. See marginalLikelihood_internal for further documentation.

Normal-Inverse-Wishart model

Described in (Bozza et al. 2008) .

Observation level:

$$X_{ij} \sim N_p(\theta_i, W_i)$$ (i = source, j = items from source)

Group level:

$$\theta_i \sim N_p(\mu, B)$$
$$W_i \sim IW_p(\nu_w, U)$$

Hyperparameters:

$$B, U, \nu_w, \mu$$

Posterior samples of $\theta$, $W^{(-1)}$ can be generated with a Gibbs sampler.

Inverted Wishart parametrization (Press)

Uses (Press 2012) parametrization.

$$X \sim IW(\nu, S)$$ with $S$ is a $p \times p$ matrix, $\nu > 2p$ (the degrees of freedom).

Then: $$E[X] = \frac{S}{\nu - 2(p + 1)}$$

References

Bozza S, Taroni F, Marquis R, Schmittbuhl M (2008). “Probabilistic Evaluation of Handwriting Evidence: Likelihood Ratio for Authorship.” Journal of the Royal Statistical Society: Series C (Applied Statistics), 57(3), 329-341. ISSN 1467-9876, doi: 10.1111/j.1467-9876.2007.00616.x .

Press SJ (2012). Applied Multivariate Analysis: Using Bayesian and Frequentist Methods of Inference. Courier Corporation.

Examples

# Use the iris data
df_X <- iris[, c(1,3)]
X <- as.matrix(df_X)
p <- ncol(X)

# Observations
plot(X)

# True species
plot(X, col = iris$Species)



# Priors
B.inv <- diag(p)
W.inv <- diag(p)
U <- diag(p)
mu <- colMeans(X)
# d.o.f.
nw <- get_minimum_nw_IW(p)

# Computational parameters
n_iter <- 10000
n_burn_in <- 1000

# Compute the marginal likelihood
marginalLikelihood(
   X = X,
   n.iter = n_iter,
   B.inv = B.inv,
   W.inv = W.inv,
   U = U,
   nw = nw,
   burn.in = n_burn_in,
   mu = mu
)
#> [1] -389.6291

# Diagnostics ------------

# Retain the full Gibbs output
list_mcmc <- marginalLikelihood(
   X = X,
   n.iter = 10000,
   B.inv = B.inv,
   W.inv = W.inv,
   U = U,
   nw = get_minimum_nw_IW(p),
   burn.in = 1000,
   mu = mu,
   output.mcmc = TRUE
)

# The log-ML value
list_mcmc$value
#> [1] -389.6172

# The full Gibbs chain output
library(coda)
head(list_mcmc$mcmc, 20)
#> Markov Chain Monte Carlo (MCMC) output:
#> Start = 1001 
#> End = 1021 
#> Thinning interval = 1 
#>        theta.1  theta.2  W.inv.1   W.inv.2   W.inv.3  W.inv.4
#>  [1,] 5.898239 3.811222 7.011690 -2.891335 -2.891335 1.555184
#>  [2,] 5.927134 3.937147 6.576140 -2.745591 -2.745591 1.489662
#>  [3,] 5.770463 3.479544 6.292374 -2.449272 -2.449272 1.282902
#>  [4,] 5.810105 3.758315 5.929512 -2.296870 -2.296870 1.207949
#>  [5,] 5.680161 3.371093 6.800086 -2.686530 -2.686530 1.349990
#>  [6,] 5.836394 3.757327 4.765470 -1.886765 -1.886765 1.051854
#>  [7,] 5.768559 3.674916 5.514650 -2.095875 -2.095875 1.056083
#>  [8,] 5.899820 3.943731 5.722077 -2.258172 -2.258172 1.188828
#>  [9,] 5.782385 3.701671 6.541726 -2.671059 -2.671059 1.420142
#> [10,] 5.849733 3.744221 6.694601 -2.737320 -2.737320 1.512495
#> [11,] 5.826484 3.843107 6.015471 -2.459960 -2.459960 1.363562
#> [12,] 5.891090 3.782015 5.184274 -2.038621 -2.038621 1.111419
#> [13,] 5.829639 3.685075 6.055362 -2.549394 -2.549394 1.436956
#> [14,] 5.841186 3.757739 5.308610 -2.186497 -2.186497 1.259971
#> [15,] 5.852877 3.754006 5.928448 -2.242769 -2.242769 1.162160
#> [16,] 5.831648 3.745047 5.485581 -2.240708 -2.240708 1.225495
#> [17,] 5.814808 3.863164 6.271212 -2.608636 -2.608636 1.416767
#> [18,] 5.885241 3.852222 5.798279 -2.310417 -2.310417 1.259523
#> [19,] 5.949191 4.022692 6.312793 -2.828027 -2.828027 1.548513
#> [20,] 5.864020 3.732325 7.045109 -2.748375 -2.748375 1.407702
#> [21,] 5.867916 3.785798 5.764394 -2.599724 -2.599724 1.532775

# Diagnostics plots by coda

plot(list_mcmc$mcmc)


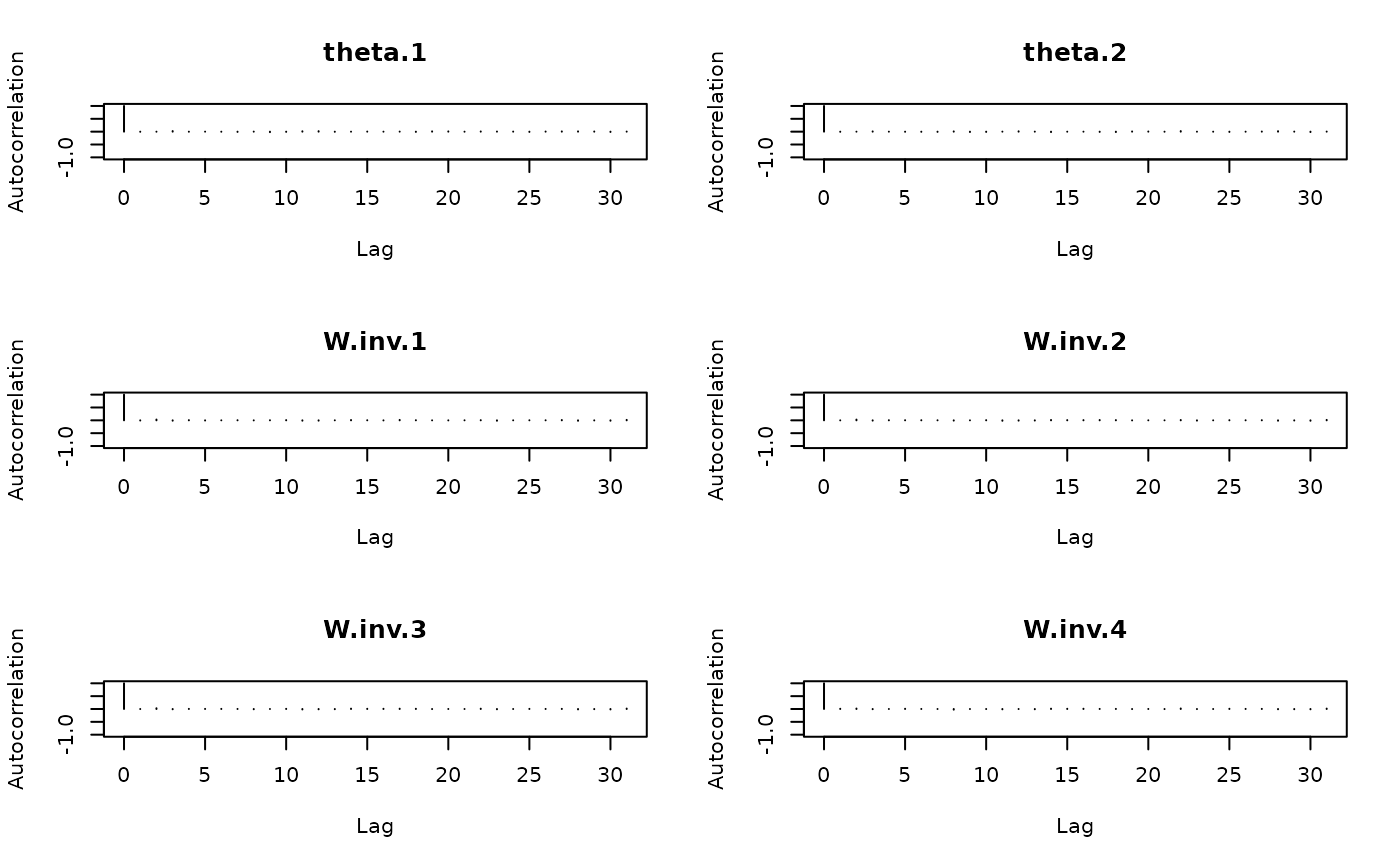
coda::autocorr.plot(list_mcmc$mcmc)

X	the observation matrix (\(n \times p\): n = observation, p = variables) @param U covariance matrix for the mean (\(p \times p\))
n.iter	number of MCMC iterations excluding burn-in
B.inv	prior inverse of between-source covariance matrix
W.inv	initialization for prior inverse of within-source covariance matrix
nw	degrees of freedom
mu	prior mean (\(p \times 1\))
burn.in	number of MCMC burn-in iterations
output.mcmc	if TRUE output the entire chain as a coda object, else just return the log-ml value
verbose	if TRUE, be verbose
Gibbs_only	if TRUE, only return the Gibbs posterior samples. Implies `chain_output = TRUE`.